Scientific Computing
Spring 2024
Mon & Wed 2:45-4:00pm
Shanahan B442
Harvey Mudd College
Zoom ID: See Canvas course site


Contact Information
Course Instructor: Professor Allon Percus
Office: CGU Math South
Phone: 909-607-0744
E-mail: 
In-person office hours: Wednesday 11am-noon
Zoom office hours: by appointment
Teaching Assistant: Kaeshav Danesh
E-mail: kdanesh@g.hmc.edu
TA office hours: Thursday 7-8pm, Shanahan B442
Course description
Math 164 aims at providing a broad range of mathematical and computational techniques for use in modeling and simulation. Topics include numerical methods for solving linear and nonlinear algebraic equations, algorithmic analysis, computer arithmetic, random number generation, Monte Carlo and optimization methods. The course is also cross-listed as CS 144 at HMC and as Math 264 at CGU.
Background Preparation (Prerequisites)
Linear algebra, ODEs, probability and statistics. Some exposure to the asymptotic analysis of algorithms is assumed (as taught in CS 60, for instance), and some basic background in mathematical analysis will help. Students should have some familiarity with Matlab but can use any standard programming language for computational assignments.
Student Learning Outcomes
By the end of this course, students will be able to:
- Understand and apply fundamental techniques of numerical analysis and computational linear algebra
- Understand probabilistic principles behind modeling, simulation, and optimization
- Comfortably, correctly, and confidently use mathematical tools for solving computational problems
Text and References
Detailed course notes, along with a number of other helpful materials, will be posted under the “Files” section on Canvas. We will frequently be referring to William H. Press, Saul A. Teukolsky, William T. Vetterling and Brian P. Flannery, Numerical Recipes: the Art of Scientific Computing, 3rd ed. (Cambridge University Press, Cambridge, 2007), available for free at http://numerical.recipes/book.html.
Class Format
Classes will consist of lectures, labs and student presentations.
Class Schedule
- Jan 17-22: Algorithms and complexity
- Jan 22-24: Computer arithmetic
Assignment #1 due - Jan 29: Root finding
- Jan 31-Feb 5: Interpolation
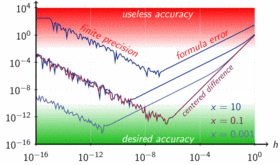
Assignment #2 due - Feb 7-12: Numerical differentiation
Assignment #3 due - Feb 12-19: Numerical integration
- Feb 19-21: Solving linear systems
Assignment #4 due - Feb 21-Mar 4: Singular value decomposition
Final project proposal due - Mar 4-6: Modeling of data
Assignment #5 due - Mar 11-13: SPRING BREAK
- Mar 18: Random number generation
- Mar 20-25: Monte Carlo
Assignment #6 due - Mar 27: LAB #1
- Apr 1-10: Markov Chains
Final project draft due - Apr 15: Simulated Annealing
- Apr 17: LAB #2
- Apr 22-24: FINAL PROJECT PRESENTATIONS
Final project due
Some classes may be recorded and made available through Canvas. Due to copyright issues, students may not circulate these recordings or distribute them outside of the class.
Assignments and Grading
Homework assignments will mostly be weekly or biweekly, depending on the week, and worth 60% of the grade. There will be a final project worth 40% of the grade. These assignments are intended not only as exercises in modeling and computing but also in scientific communication. Pay attention to clarity, grammar and spelling. All assignments will be posted on Gradescope as well as under the “Assignments” section on Canvas. You will submit them in PDF format on Gradescope, except for code which you will upload to Canvas, unless otherwise specified.
You are welcome to collaborate on assignments, subject to a few basic rules:
- Collaborate to understand the problem better – not just to get the (right) answer.
- Do not look at someone else’s code until you have written your own, and it works.
- Write up your submission individually, and in your own words, unless the assignment specifically calls for a team submission.
- Acknowledge all sources of help (people, books, websites, etc.) that you receive to complete your work. You must list the names of all of your collaborators.
- Do not simply correct the work or debug the code of others: by offering to collaborate, you take responsibility for helping them understand what is involved.