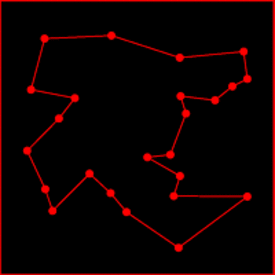
Given n points (“cities”) with random distances between them, what are the properties of the shortest closed path (“tour”) passing through all the cities?
Our numerical estimates from 1996 for the 2- and 3-dimensional traveling salesman constant are still the most precise ones to date, along with simultaneous results by David Johnson, et al. David Aldous and I have also studied how the length of a tour scales under small perturbations from optimality. This property appears to classify discrete optimization problems into a small number of distinct categories, reminiscent of universality classes in physics. Finally, for the non-metric problem where lengths between cities are i.i.d. random variables, ongoing work using the cavity method is leading to a precise conjecture on the probability with which an optimal tour connects a city to its kth neighbor.
- C. Wang, J.D. Hyman, A.G. Percus and R. Caflisch, “Parallel tempering for the traveling salesman problem,” International Journal of Modern Physics C 20, 539-556 (2009).
- A.G. Percus, “The traveling salesman problem and kth-nearest neighbors,” Los Alamos report LA-UR 06-6896 (2006).
- D. Aldous and A.G. Percus, “Scaling and universality in continuous length combinatorial optimization,” Proceedings of the National Academy of Sciences 100, 11211-11215 (2003).
- A.G. Percus and O.C. Martin, “The stochastic traveling salesman problem: Finite size scaling and the cavity prediction,” Journal of Statistical Physics 94, 739-758 (1999).
- A.G. Percus and O.C. Martin, “Scaling universalities of kth-nearest neighbor distances on closed manifolds,” Advances in Applied Mathematics 21, 424-436 (1998).
- N.J. Cerf, J. Boutet de Monvel, O. Bohigas, O.C. Martin and A.G. Percus, “The random link approximation for the Euclidean traveling salesman problem,” Journal de Physique I 7, 117-136 (1997).
- A.G. Percus and O.C. Martin, “Finite size and dimensional dependence of the Euclidean traveling salesman problem,” Physical Review Letters 76, 1188-1191 (1996).
- A.G. Percus, The Traveling Salesman and Related Stochastic Problems. Ph.D. thesis, Université Pierre et Marie Curie, Paris (1997).